Pytorch的torch.matmal()详解
torch.matmal()功能简介
torch.matmul()方法是用于执行矩阵乘法(matrix multiplication)的操作,几乎可以用于所有矩阵/向量相乘的情况,其乘法规则视参与乘法的两个张量的维度而定。这个方法是PyTorch中进行线性代数计算的常用方法之一。
torch.matmul() 将两个张量相乘划分成了五种情形:一维 × 一维、二维 × 二维、一维 × 二维、二维 × 一维、涉及到三维及三维以上维度的张量的乘法。
使用方法
torch.matmul(input, other, *, out=None) -> Tensor
- input (Tensor) – 第一个输入张量。
- other (Tensor) – 第二个输入张量。
- out (Tensor, optional) – 用来存储输出结果的张量。
一维乘以一维
如果两个张量都是一维的,即 torch.Size([n]) ,此时返回两个向量的点积。作用与 torch.dot() 相同,同样要求两个一维张量的元素个数相同。
示例代码:
import torch vec1 = torch.tensor([1, 2, 3]) vec2 = torch.tensor([2, 3, 4]) vec_result = torch.matmul(vec1, vec2) print(vec_result) # 输出结果为tensor(20)
两个一维张量的元素个数一定要相同,否则会报错。
示例代码:
import torch vec1 = torch.tensor([1, 2, 3]) vec2 = torch.tensor([2, 3, 4, 5]) vec_result = torch.matmul(vec1, vec2) print(vec_result)
执行上述代码则会报错如下:
RuntimeError: inconsistent tensor size, expected tensor [3] and src [4] to have the same number of elements, but got 3 and 4 elements respectively
二维乘以二维
如果两个参数都是二维张量,那么将返回矩阵乘积。作用与 torch.mm() 相同,同样要求两个张量的形状需要满足矩阵乘法的条件,即:
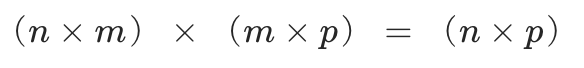
示例代码:
import torch
# 二维乘以二维
arg1 = torch.tensor([[1, 2], [3, 4]])
arg2 = torch.tensor([[-1], [2]])
r = torch.matmul(arg1, arg2)
print(f'二维乘以二维:{r}')
一维乘以二维
如果第一个参数是一维张量,第二个参数是二维张量,那么在一维张量的前面增加一个维度,然后进行矩阵乘法,矩阵乘法结束后移除添加的维度。
文档原文为:“a 1 is prepended to its dimension for the purpose of the matrix multiply. After the matrix multiply, the prepended dimension is removed.”
import torch
# 一维乘以二维
arg1 = torch.tensor([-1, 2])
arg2 = torch.tensor([[1, 2], [3, 4]])
r = torch.matmul(arg1, arg2)
print(f'一维乘以二维:{r}')
二维乘以一维
如果第一个参数是二维张量(矩阵),第二个参数是一维张量(向量),那么将返回矩阵×向量的积。作用与 torch.mv() 相同。另外要求矩阵的形状和向量的形状满足矩阵乘法的要求。
import torch
# 二维乘以一维
arg1 = torch.tensor([[1, 2], [3, 4]])
arg2 = torch.tensor([-1, 2])
r = torch.matmul(arg1, arg2)
print(f'二维乘以一维:{r}')
高纬张量乘法
如果两个参数均至少为一维,且其中一个参数的 ndim > 2,那么需要进行一番处理之后,再进行批量矩阵乘法。
这条规则将所有涉及到三维张量及三维以上的张量(下文称为高维张量)的乘法分为三类:一维张量 × 高维张量、高维张量 × 一维张量、二维及二维以上的张量 × 二维及二维以上的张量。
1、如果第一个参数是一维张量,那么在此张量之前增加一个维度。
“If the first argument is 1-dimensional, a 1 is prepended to its dimension for the purpose of the batched matrix multiply and removed after.”
2、如果第二个参数是一维张量,那么在此张量之后增加一个维度。
“If the second argument is 1-dimensional, a 1 is appended to its dimension for the purpose of the batched matrix multiple and removed after. ”
3、由于上述两个规则,所有涉及到一维张量和高维张量的乘法都被转变为二维及二维以上的张量 × 二维及二维以上的张量。
然后除掉最右边的两个维度,对剩下的维度进行广播。“The non-matrix dimensions are broadcasted.”
然后就可以进行批量矩阵乘法。
For example, if input is a (j × 1 × n × n) tensor and other is a (k × n × n) tensor, out will be a (j × k × n × n) tensor.
示例如下:
arg1 = torch.tensor([1, 2, -1, 1])
arg2 = torch.randint(low=-2, high=3, size=[3, 4, 1])
print(arg2)
r = torch.matmul(arg1, arg2)
print(f'高纬相乘结果:{r}')
其他示例
二维矩阵乘法:
import torch # 定义两个二维矩阵 a = torch.tensor([[1, 2], [3, 4]]) b = torch.tensor([[5, 6], [7, 8]]) # 使用 matmul 进行矩阵乘法 result = torch.matmul(a, b) print(result) # tensor([[19, 22], # [43, 50]])
高维度张量的批量矩阵乘法:
import torch # 定义两个三维张量 a = torch.randn(2, 3, 4) b = torch.randn(2, 4, 5) # 使用 matmul 进行批量矩阵乘法 result = torch.matmul(a, b) print(result.shape) # torch.Size([2, 3, 5])
广播机制:
当输入的维度不匹配时,自动进行广播(broadcasting)。
import torch # 定义一个二维矩阵和一个三维张量 a = torch.tensor([[1, 2], [3, 4]]) b = torch.randn(2, 2, 3) # 使用 matmul 进行矩阵乘法,自动广播 result = torch.matmul(a, b) print(result.shape) # torch.Size([2, 2, 3])
注意事项
- 输入张量的最后两个维度必须是可乘的,即
input.shape[-1] == other.shape[-2]。 - 如果输入张量的维度大于2,需要注意其批处理维度。
matmul方法在深度学习及其他需要进行线性代数计算的领域非常有用,特别是面对多维数据时。这使得计算更加简洁和高效。

关注公众号:程序新视界,一个让你软实力、硬技术同步提升的平台
除非注明,否则均为程序新视界原创文章,转载必须以链接形式标明本文链接